现代密码学大作业:RSA大礼包
RSA 大礼包解题报告
由于之前根本没有学过密码分析学的相关知识,自身主攻方向也不在密码学,所以这些东西都只能现学现用。
根据群里dbt和群友给出的提示,算是有了一个比较明确的解题方向。那么就一步一步开始吧。
首先我找到了一个老学长的博客,可以从他那里学到一点东西背景知识。
| 攻击方法 | 破解模数 | 破译明文 |
|---|---|---|
| 费马分解 | Frame10 | Frame10 |
| Pollard p-1 分解 | Frame2、6、19 | Frame2、6、19 |
| 低加密指数攻击 | 无 | Frame3、8、12、16、20 |
| 公共模数攻击 | 无 | Frame0、4 |
| 因数碰撞 | Frame1、18 | Frame1、18 |
| 猜测明文攻击 | 无 | Frame5、7、9、11、13、14、15、17 |
| 随机数发生器攻击 | Frame0、3、4、5、7、8、9、11、12、13、14、15、16、17、20 | 验证全部明文正确性 |
看完赛题说明,可以发现本题中的RSA体系使用的是最原始的教科书式RSA,没有经过哈希的RSA肯定的是不符合加密标准的,这也是最根本的问题。同时通信人Alice可能重复发送明文片段的问题,也会成为解密的突破口。


然后我使用一个脚本,根据赛题中给出的格式信息,对每一帧数据进行分类。
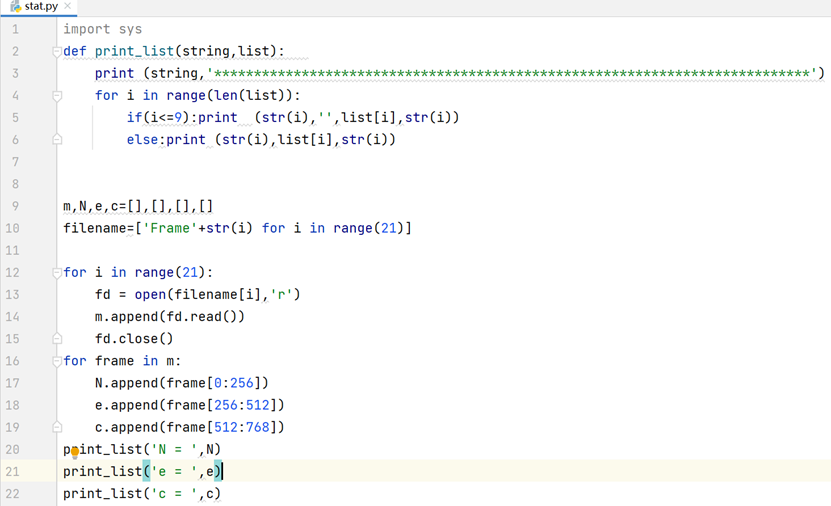
得到的结果如下:
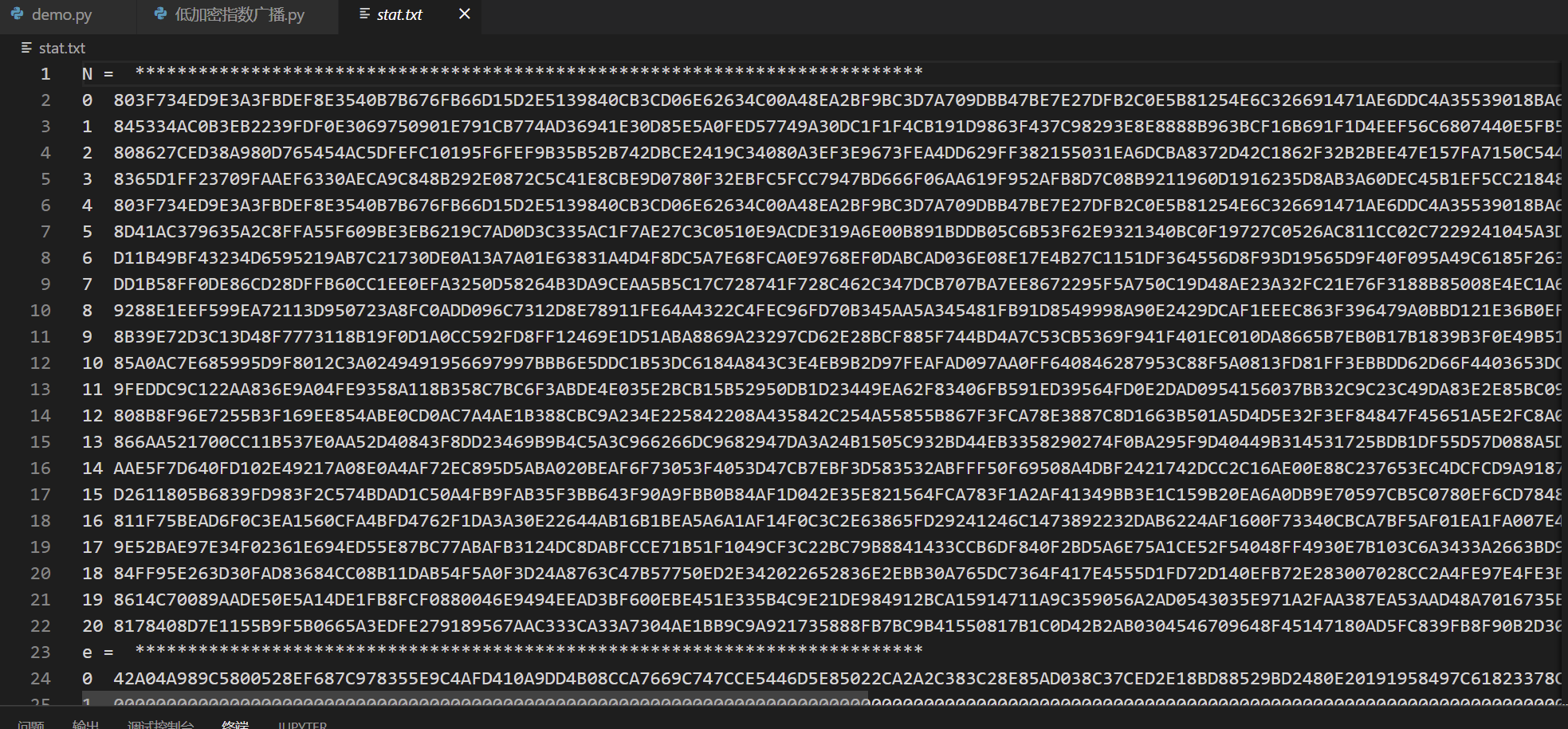
低加密指数攻击
经过对每一帧的数据检查可以发现,加密指数e的取值一共有3、5、65537、以及一些较大的数。比较小的e可以加快加密时间,但是也会增大被破解的风险。其中Frame3、8、12、16、20是使用的e = 5,所以可以据此进行低加密指数广播攻击。
而广播攻击的原理是中国剩余定理,信安数基已有过详细学习,这里不再赘述。具体的代码实现放在附件中,经过这一步我们可以得到:
解密是0x9876543210abcdef0000000100000000000000000000000000000000000000000000000000000000000000000000000000000000000000007420697320612066
由此确定这段明文属于第二段,还原字符串得到:

核心代码如下:
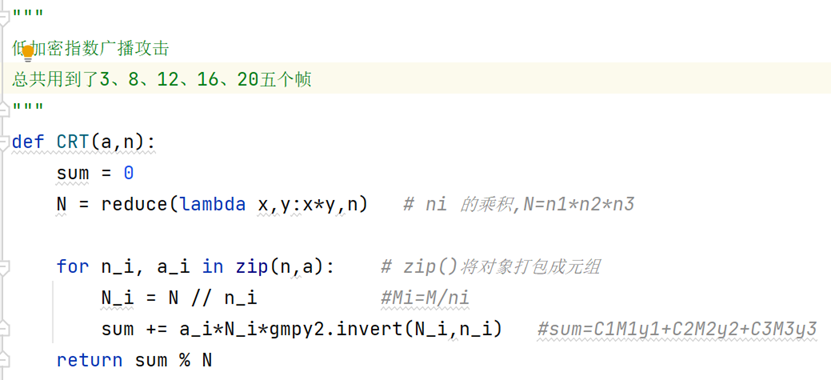
Fermat 分解法
之后应该从哪里入手呢,尝试对Frame10使用Fermat分解法。费马分解主要是对大整数的分解。其中Fermat主要是在p,q相差不大时效率比较高。具体如图:

代码描述如下:


这段明文就是will get。
Pollard p-1 分解
Pollard p-1分解和费马分解比较类似,都是基于大整数分解的思路。但是相对而言,Pollard就更适用于p和q相差比较大的情况。
具体操作如下:
l 已知整数n,找到一个因数d|n
l 先固定大整数B
l 选择一个整数k,1~k的累积不大于B,如k=B!
l 随机选择整数a满足2<=a<=n-2 我们选择2
l 计算r = a^k mod n
l 计算d = gcd(r-1,n)
l 如果d = 1 或者 d = n,则重新选择k,否则输出d
其实也就是一个循环。
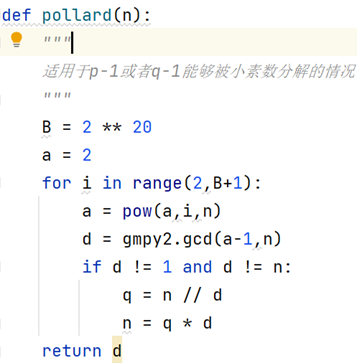
可以得到如下结果:

按照顺序排列是:+instein.+
+ “Logic +
+ That is+
从语感的角度来说,instein应该是某个人名,然后首先想到的就是Einstein,难道这个原文会和他说的话有关系吗?当然这就脱离密码学了。
公共模数攻击
接着我们发现,Frame0和Frame4使用了同一个模数N,由此存在公共模数攻击,可以解开一段明文。以下是共模攻击原理:

代码实现如下:
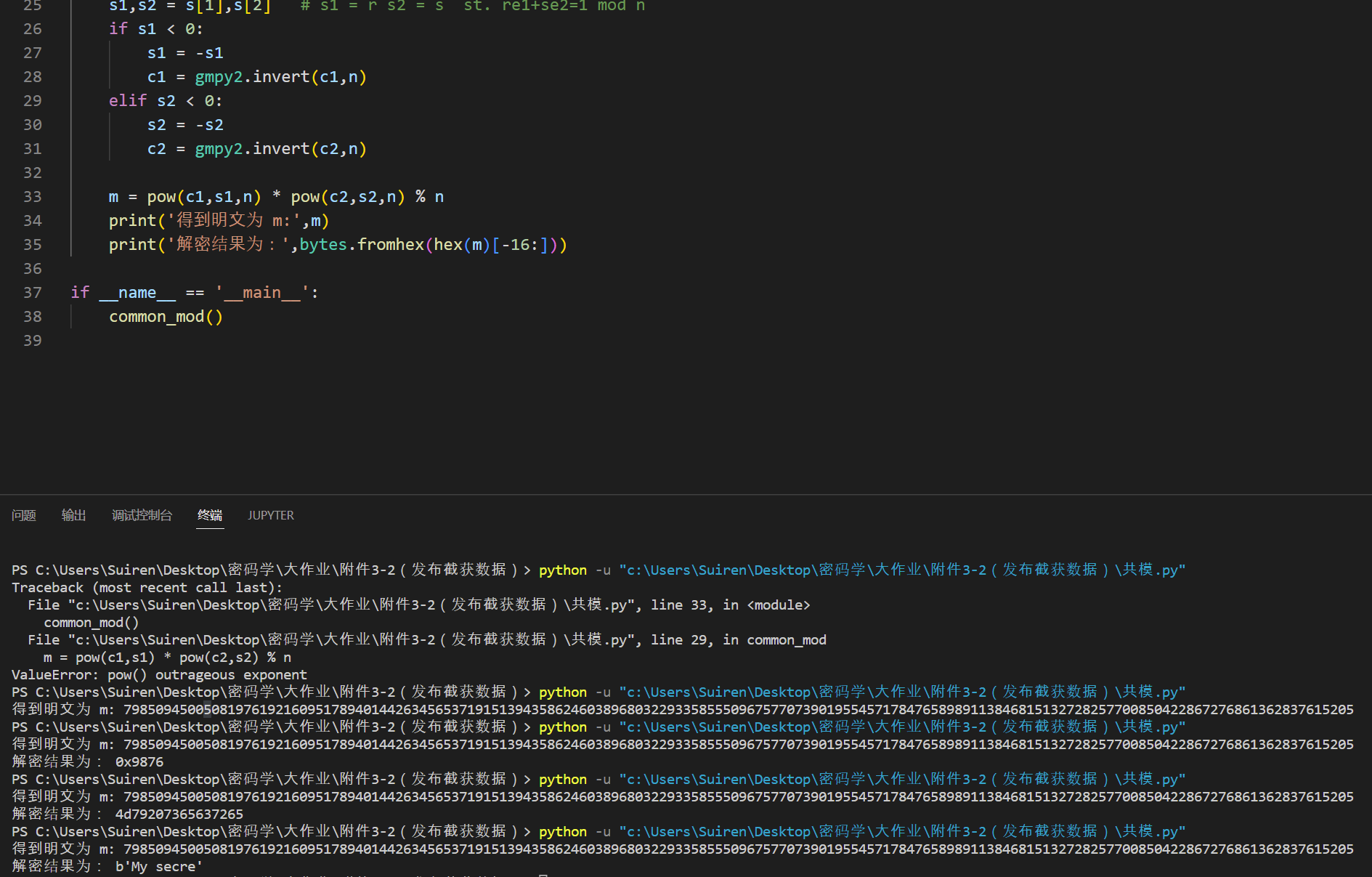
得到明文片段 My secre
因数碰撞攻击
几种比较简单的攻击方式到这里就做完了。根据提示,下一种要看的是因数碰撞攻击。提示中已经给出了存在碰撞的是Frame1和Frame18,这就省去了我们遍历尝试的时间了。
而因数碰撞攻击的原理也很简单:如果两个模数存在公共因子,则可以通过简单的乘除处理进行模数分解,最终破解出两个模数对应的明文。
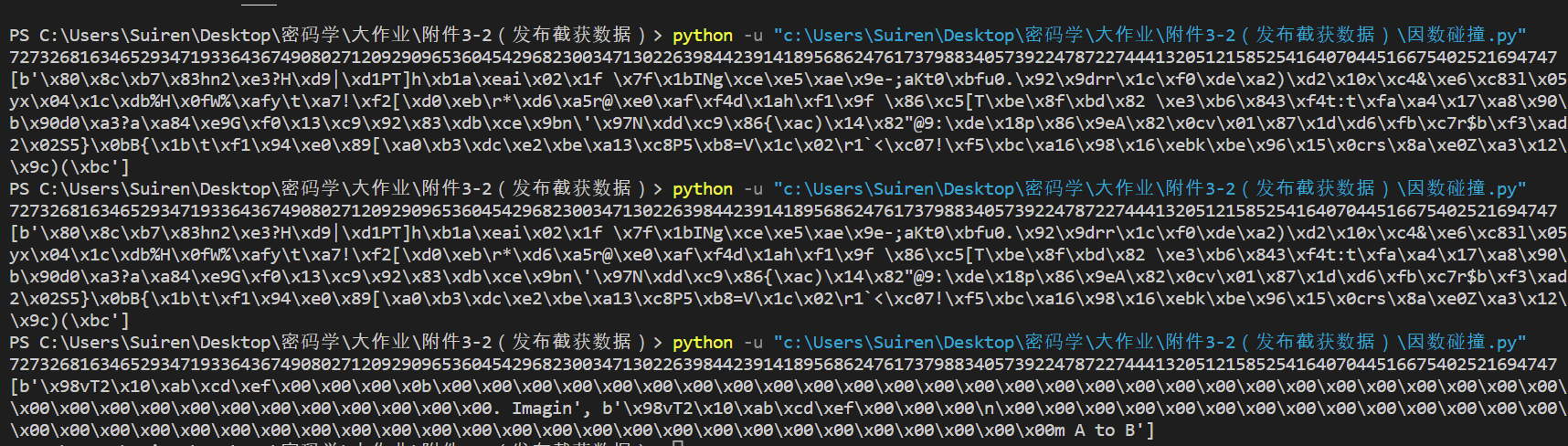
在解出这一部分过程中,发现了学长的博客中存在问题,对程序进行排查后,根据原理,反复尝试解出了原文,一共有两段。
. Imagin| ——很明显就是Imgaine
m A to B| ——按照语感应该是From A to B
猜测明文
到此为止,已经解出的明文有:
My secre
t is a f
will get
instein.
“Logic
That is
.Imagin
m A to B
按照英文语感来说,这应该是爱因斯坦说过的,关于想象力的名句,然后网上搜索。

确实是这种熟悉的感觉。
Ok到这里,爱因斯坦到底有没有说过这句话,已经不重要了。
由于英文中会写出名人的全称,所以Einstein 前必然有 Albert。
进行原文重组,就是:
My secret is a f________ Albert Einstein. That is “Logic will get you from A to B. Imagination will take you everywhere.”
到此还有一段引文没有解出,是一个f开头的单词,而他引用的又是一段名句。那么合理猜测后面肯定还有一段 saying of (Albert…).所以f开头的很大概率就是一个形容词,修饰名句本身,那么很容易想到famous。
综合以上可以得到最终的答案:
My secret is a famous saying of Albert Einstein. That is “Logic will get you from A to B. Imagination will take you everywhere.”
总结
本次大作业对应的是公钥密码学的RSA公钥密码体系,需要用的知识和技能是Dan Boneh 的课堂上学不到的,对于我来说确实是很大的挑战。刚开始解决这些问题时,每一点小小的进展都很不容易,接触到的那些完全陌生的方法、术语以及网络上贫瘠的参考资料让我头疼,技术还是不太行啊。
总体来看,这些针对RSA脆弱性的攻击,究其原因其实是在体系上使用了教科书式RSA的问题。这也是在Dan Boneh的课堂上重点强调过的一点,例如共模攻击,直接使用了公钥来加密明文,因此产生了严重的攻击。所以在实际的使用中,RSA公钥体系必须采取相应标准才能确保机密性。
解完这些puzzles大概用了我一周的时间,每天上完课后去lib如同打卡上班,开始今天的新攻击。最终还是克服了不求甚解,一知半解的心理,把每一种攻击方法都看完了。密码学真的很神奇。
